← Back to Homepage

Leveraging Hidden Markov Models for Regime-Based Segmentation in Time-Series

Nov 16, 2024

A technical exploration of how Hidden Markov Models can reveal underlying patterns in complex time series data

The Power of State-Space Models

Time series data is everywhere — financial markets, weather patterns, and speech signals. But analyzing it isn’t always straightforward, especially when hidden factors drive the observed data. Hidden Markov Models (HMMs) are a statistical tool that can uncover these hidden states, making them invaluable for tasks like regime detection in financial markets. In this article, we’ll explore what HMMs are, how they work, and how traders can use them to identify market regimes and improve their strategies.

Understanding Hidden Markov Models

HMMs are models used to describe systems that transition between hidden states over time. Each hidden state produces observable outputs according to specific probabilities. The model consists of three main parts: transition probabilities (how likely it is to move between states), emission probabilities (how likely each state is to produce specific observations), and initial probabilities (the likelihood of starting in a particular state). HMMs are widely used in fields like speech recognition, bioinformatics, and financial market analysis because they can model complex, sequential patterns effectively.

At its core, an HMM is a state-space model that combines two stochastic processes:

  1. The Hidden Process: A Markov chain representing the underlying states
    aij = P(qt+1 = j | qt = i)
  2. The Observable Process: The emission distributions for each state
    bj(ot) = P(ot | qt = j)

The model’s power comes from its ability to capture both the temporal dependencies through the Markov property and state-specific behavior through emission distributions.

Regime-Based Segmentation in Trading

In trading, regime-based segmentation means dividing the market into distinct phases or conditions, such as bullish, bearish, or sideways trends. Identifying these regimes is crucial because markets behave differently under each condition. For example, a strategy that works in a bullish market might fail in a bearish one. HMMs help traders uncover these hidden regimes, even when they aren’t directly observable.

Implementation and Estimation

The implementation of HMMs involves several key steps:

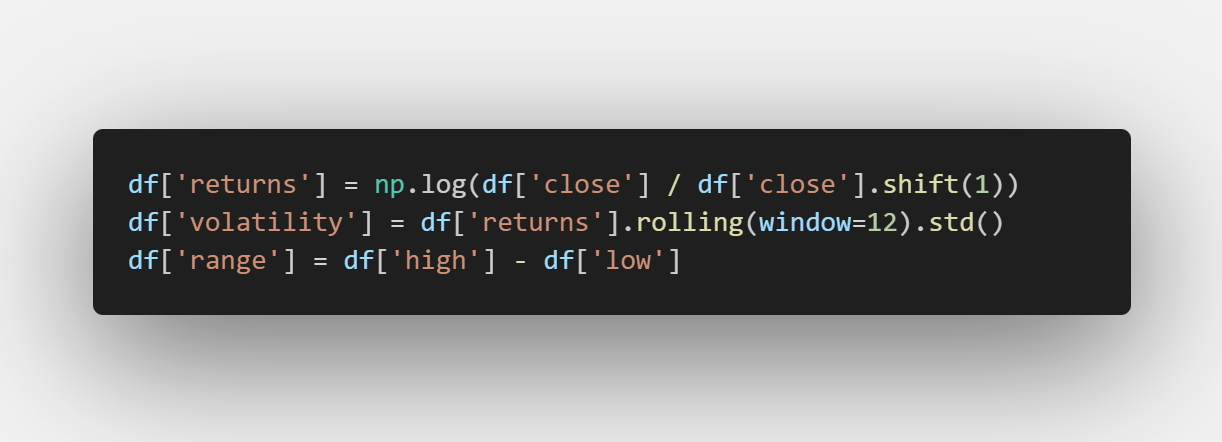
Feature Engineering

Key features for state detection:

HMM Implementation Code
Sample Python code for implementing HMM

Model Estimation

hmm model
hmm model

Parameter Learning

The model parameters are typically estimated using:

State Identification

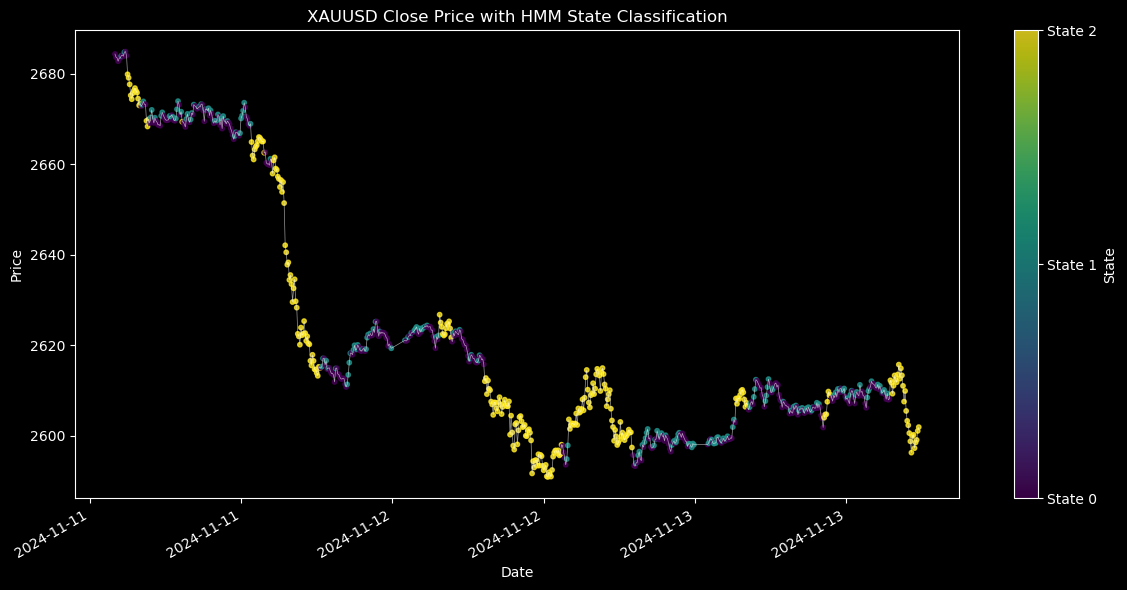
The analysis of the time series revealed three distinct market regimes. State 0, the stationary regime, is characterized by low temporal dependence, a stable variance structure, and a returns distribution resembling a Gaussian curve. State 1, the transitional regime, shows moderate serial correlation, shifting variance patterns, and a skewed returns distribution, indicating a phase of market adjustment. Finally, State 2, the dynamic regime, is marked by strong temporal dependence, heteroskedastic (changing) variance, and a heavy-tailed returns distribution, often reflecting periods of high volatility and significant market shifts.

Figure 1: Time series segmentation using HMM state classification
Figure 1: Time series segmentation using HMM state classification

Validation ensures the Hidden Markov Model (HMM) is reliable and effective. Techniques like AIC, BIC, and likelihood ratio tests help determine the optimal number of states, while cross-validation ensures the model generalizes to new data. Residual analysis checks for unmodeled patterns, and state stability testing ensures consistent regime assignments. Goodness-of-fit tests and predictive performance evaluations confirm the model’s accuracy and practicality for tasks like market regime detection.

Conclusion

HMMs are a powerful tool for uncovering hidden structures in time series data, making them highly useful for tasks like market regime detection. Beyond finance, these models are equally valuable in fields like economics, where they identify growth or recession periods, and in climate science, where they help analyze weather patterns and climate shifts. In biology, they assist in decoding genetic sequences, while in speech recognition, they enable accurate modeling of spoken language. By applying HMMs, traders and professionals across disciplines can better understand complex systems and make informed decisions. If you’re curious, explore Python libraries and try applying HMMs to your data to uncover insights.